Ретро мат в 2 хода

Задачи онлайн

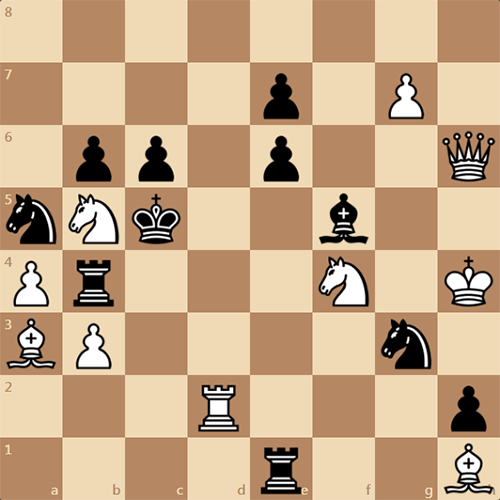
Задача на ретро мат в 2 хода. Ее автор Нильс Хаег. Задача опубликована в 1924 году в журнале "Chess Amateur".

Смысл задач на ретро мат такой: черные и белые по очереди берут назад свои ходы, а затем в возникшей позиции белые могут поставить мат в 1 ход. Такие задачи очень сложны для решения, но от того они и интересней.

Нильс Хаег по профессии офтальмолог, как проблемист стал известен с 1923 года и преуспел в этом деле. Им составлено около 700 рертрозадач на различные темы. Его задачи очень трудны.

9 комментариев

1 076 просмотров

Комментарии 9

G.E.

Это защитный ретрактор, тип Høeg (не знаю, правильна ли транскрипция у slonikа).
Когда одна сторона берет ход назад, другая сторона выбирает, было ли при этом взятие и какая именно фигура была побита. То есть, если белые, например, просто возьмут назад ход Cb1-a2, то черные могут заявить: на a2 вы побили нашего ферзя - и окажется, что ход Kb3# это и не мат вовсе.

(Я бы не стал предлагать подобную задачу для решения, тем более, что в ней был найден дефект.)

17 марта 2020 17:03
0
Ser1405

Цитата: G.E.
G.E.

Кроме того , Слоник сформулировал таким образом, что последний ход делали чёрные , а здесь такого вроде как не должно было быть...

17 марта 2020 17:41
0
G.E.

Имеется в виду такая последовательность: белые берут ход назад - черные берут ход назад - белые берут ход назад: и белые ходят, давая мат. Все позиции в ходе решения должны быть легальными (т.е. могли получиться из начальной позиции и не противоречат правилам шахмат).

---добавление
В настоящее время известны три типа защитных ретракторов.

Høeg retractor (взятие определяет оппонент)
Proca retractor (ход полностью определяется одной стороной)
Pacific retractor (взятия в ретроигре недопустимы)

17 марта 2020 18:22
0
Сергей Иванович

Я так понял, что автор предполагал предпоследними ходами взятия на поле g3: черной фигурой 8-мой белой пешки и пешкой h2:g3. Тогда для размещения белых пешек (a2-f7. b2-c4. c2-h7. e2-g4 и h2:g3) нужно 14 ходов-взятий и, следовательно, у черных ничего не могло быть на поле а2. Вместо 1.Сb1-a2 белые обявляют мат 1.Kb3Х.

Но, кажись, и после f2:g3 нужно 14 ходов-взятий (a2-f7. b2-c4. c2-h7. e2-f3. h2-g4 и f2:g3)

А еще возражение могло бы быть таким: если у черных осталась бы хоть одна фигура, то она может стоять на поле b1 и последним не мог быть ход 1.Сb1-a2...

17 марта 2020 19:11
0
Basilio

Цитата: Сергей Иванович
А еще возражение могло бы быть таким: если у черных осталась бы хоть одна фигура, то она может стоять на поле b1 и последним не мог быть ход 1.Сb1-a2...

Я нашел в интернете журнал от 1928 года со статьёй этого самого Хэега :
http://ruchess.ru/upload/iblock/356/356e9929625b2b2213fb60afe9fc37ef.pdf
Он описывает придуманные им же правила решения таких задач. Там получается, что чёрные могут ставить фигуры только на поля, с которых белые убрали свою.
Кстати, данная задача там в качестве примера (стр. 15-17).

17 марта 2020 19:44
0
Сергей Иванович

Цитата: Basilio
журнал от 1928 года
Это пятый выпуск из сборника "Задачи и этюды", состоящего из восьми выпусков (1927-1930гг.) и переизданного под редакцией О.Первакова в 2015 году. Видимо, отсюда Slonik и почерпнул сведения о N.HOEG и его задаче.

17 марта 2020 20:16
0
Ильф

Попалась занятная ретрозадачка для начинающих. Белые: пе4, белопольного слона нет, остальные в начальной позиции. Чёрные: пс6, пе6, пешка d отсутствует, остальные в начальной позиции. Нужно повторить партиюю, в которой белые и чёрные сделали по 4 хода

18 марта 2020 10:49
-1
slonik

Цитата: Ильф
Ильф

Так была же ранее уже!

https://chessok.net/zadachi/999-originalnaya-shahmatnaya-zadacha.html

18 марта 2020 11:18
0
Ильф

Цитата: slonik
Так была же ранее уже!
Понял??‍♂️?

18 марта 2020 12:00
0

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации. Зарегистрируйтесь. Кнопка регистрации есть справа вверху.

Другие статьи

Ретро мат в 2 хода

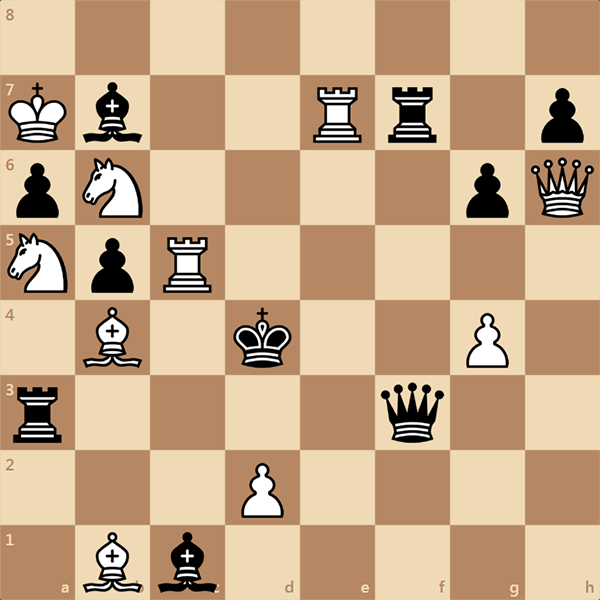
Мат в 3 хода. Автор задачи К. Ганнеман

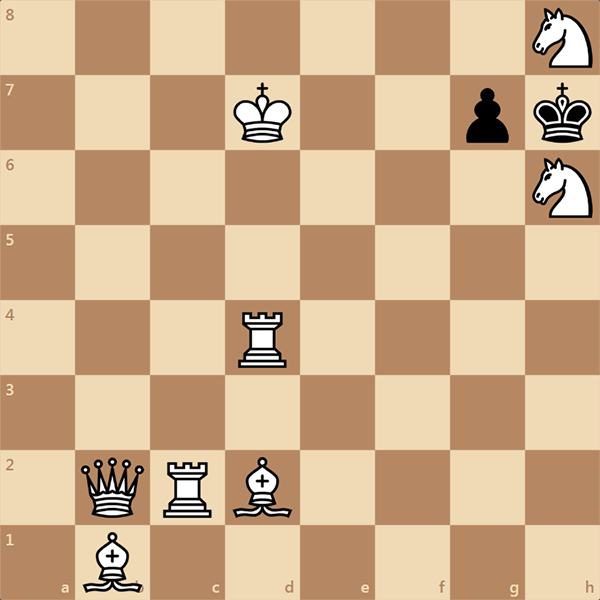
Мат в 2 хода, задача Ф. Гемеджа

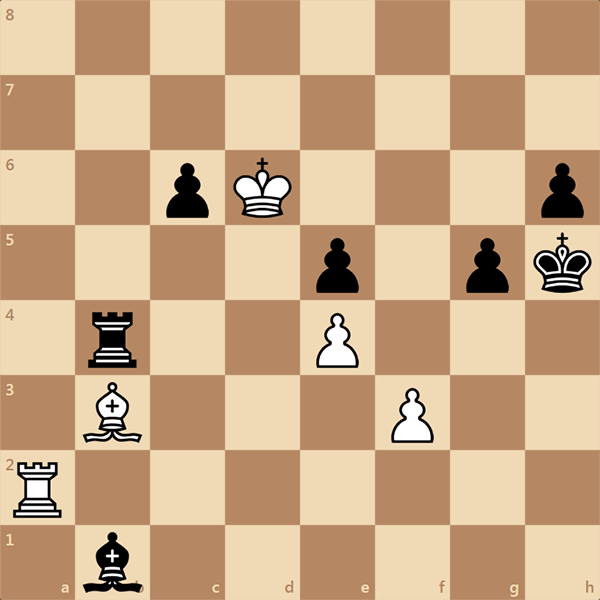
Задача на кооперативный мат в 2 хода

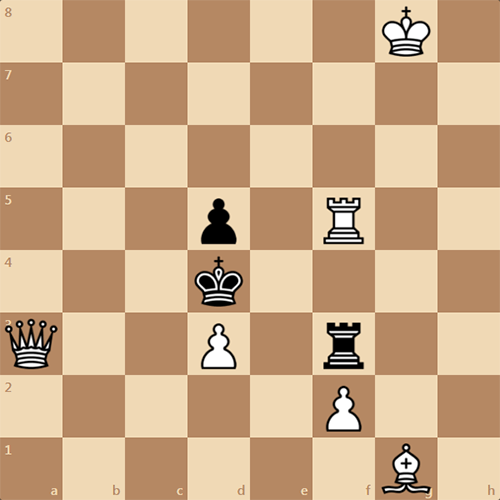
Мат в 2 хода. Задача 1915 года

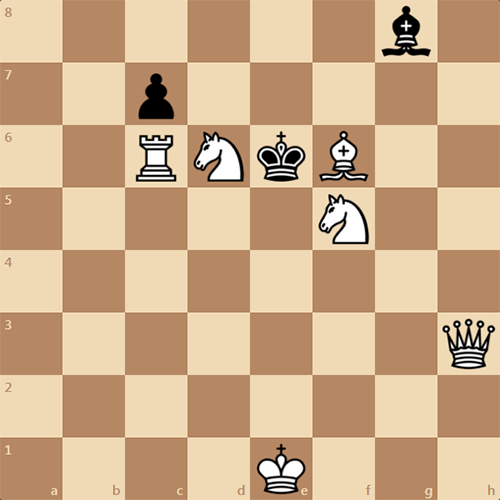
Мат в 2 хода У. Кларка

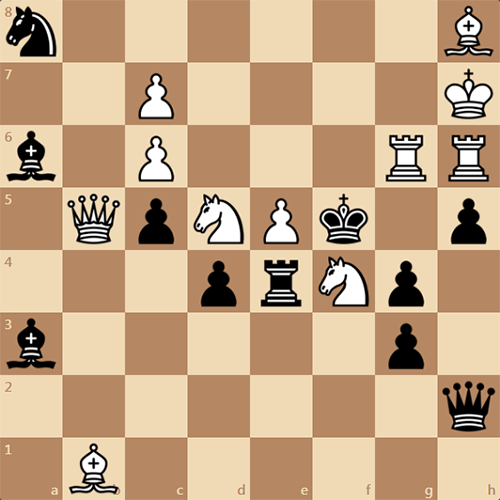
Содержательная задача 1998 года

Интересный мат в 2 хода, автор задачи А. Мари