Турниры
10-ка лучших шахматистов мира
Магнус КарлсенНорвегия
2864
Дин ЛижэньКитай
2806
Алиреза ФируджаФранция
2793
Каруана ФабианоСША
2783
Левон АронянРоссия
2775
Уэсли СоСША
2773
Ян НепомнящийРоссия
2766
Рихард РаппортВенгрия
2764
Аниш ГириНидерланды
2760
Максим Вашье-ЛагравФранция
2760
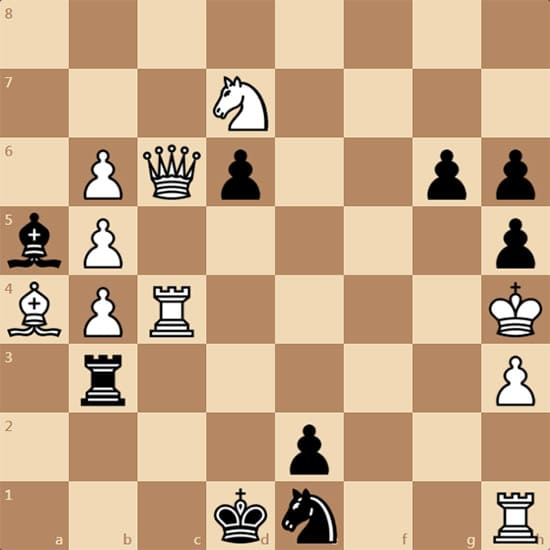
Обратный мат в 2 хода (AP) Максимуммер, автор А. Василенко

Элси: "Задача даже премию получила. И по моему мнению - с в корне неверным и некорректным решением. Правда, у задачи есть и корректное нормальное решение. Автор Анатолий Василенко, Die Schwalbe 132 12/1991, 4. Lob. Обратный мат в 2 хода (AP) Максимуммер".
592 просмотров
Комментарии 71
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации. Зарегистрируйтесь. Кнопка регистрации есть справа вверху.
Другие статьи
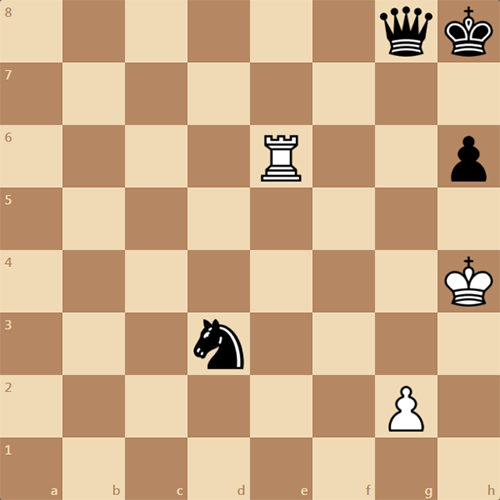
Приличная задача, в которой начинают белые и ставят мат в 2 хода. Автор Анатолий Василенко. Опубликована в 2020 году.
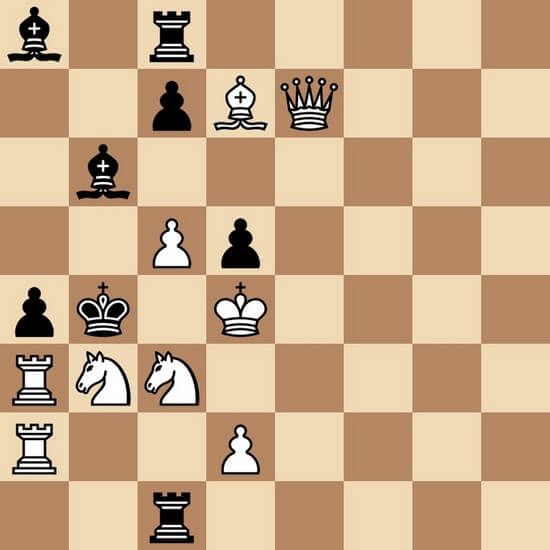
Да, эта задача 2020 года. Свежак :) Обратный мат в 2 хода. Максимуммер. Автор задачи Анатолий Степочкин.

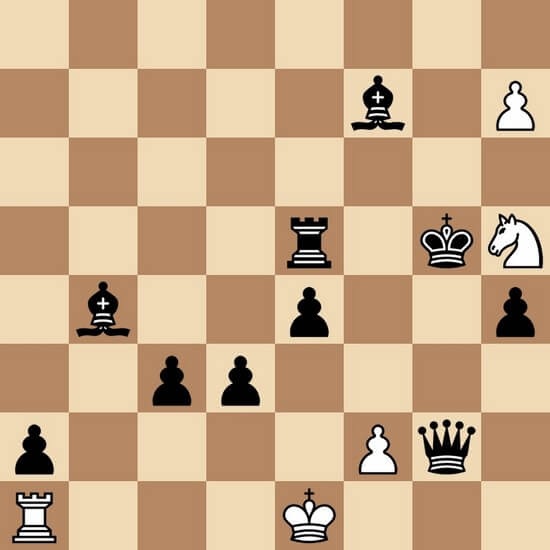
Обратный мат в 4 хода, максимуммер. Как решите, переставляйте слона с c1 на d2 и решайте с тем же условием. Задача опубликована в 1958 году.
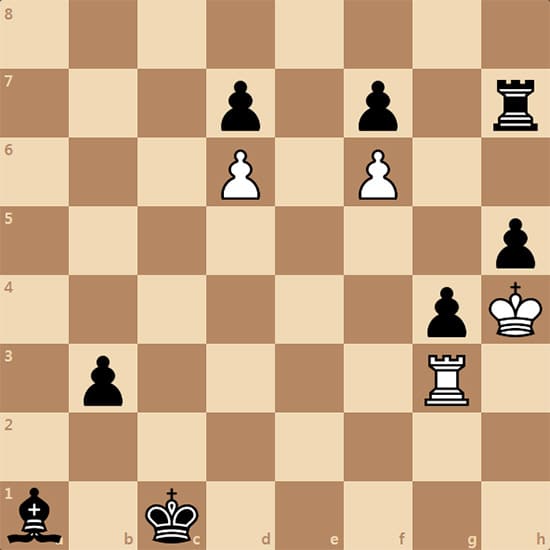
Задача 1980 года. Обратный мат в 9 ходов - максимуммер. Автор задачи Theodor Tauber. Фата-моргана...
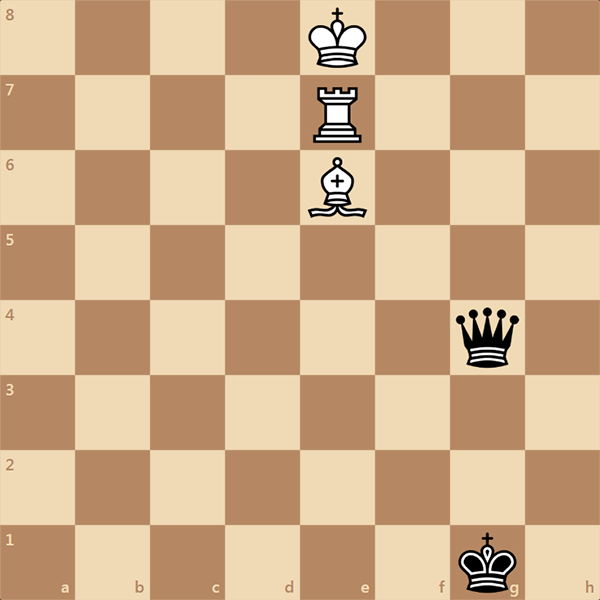
Задача на обратный мат в 5 ходов, автор которой А. Степочкин. Вся суть в том, что это максимуммер. Это означает, что в процессе решения черные обязаны делать самые длинные ходы. У нас уже была подобная задача. Ее можно найти