Турниры
10-ка лучших шахматистов мира
Магнус КарлсенНорвегия
2864
Дин ЛижэньКитай
2806
Алиреза ФируджаФранция
2793
Каруана ФабианоСША
2783
Левон АронянРоссия
2775
Уэсли СоСША
2773
Ян НепомнящийРоссия
2766
Рихард РаппортВенгрия
2764
Аниш ГириНидерланды
2760
Максим Вашье-ЛагравФранция
2760
Мат в 1 ход. Коэффициент Бергера
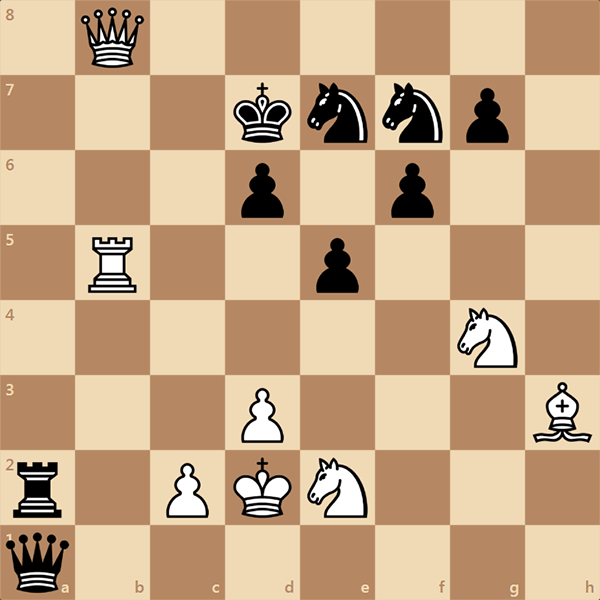
Опубликовали для вас еще одну хорошую статью. Не могли не добавить задачу, ну вы знаете :) Белые начинают и ставят мат в 1 ход.
Нередко в турнирах по шахматам некоторые участники могут заработать равное количество очков. В целях определения в этом случае места в турнирной таблице шахматистов и служит вышеуказанный коэффициент. Определяется он следующим образом:
берём двух шахматистов-участников кругового турнира, которые набрали одинаковое количество очков. Затем суммируем все итоговые очки шахматистов, у которых каждый выиграл. Это будет первая сумма. Потом складываются таким же образом очки тех шахматистов, с которыми они сделали ничью. Эту сумму делим пополам. Это будет вторая сумма. Потом складываем первую и вторую сумму. Так высчитывается коэффициент Бергера.
У кого он выше - тот и расположится выше в турнирной таблице. Иными словами, преимущество получает тот, кто в ходе соревнований одерживал победы над более сильными соперниками. Пояснить логику такого выбора можно на простом примере.
Скажем, первый шахматист проиграл слабому шахматисту, который занял одно из последних мест в турнирной таблице, и выиграл у сильного шахматиста - победителя соревнований. Второй же шахматист выиграл у этого же слабого шахматиста, но проиграл шахматисту, занявшему первое место.
В этом случае преимущество получает первый шахматист, победивший чемпиона. Если возникает необходимость, то данный коэффициент может применяться не только в соревнованиях шахматистов по круговой системе, но и по швейцарской.
В заключение хочется отметить, что идея коэффициента принадлежит не Бергеру, а жителю Чехии Оскару Гельбфусу. Бергер просто практически реализовал данную идею на турнире 1882 года в Ливерпуле.
Посмотрите статью про коэффициент Бухгольца - тоже интересно.
7 427 просмотров
Комментарии 2
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации. Зарегистрируйтесь. Кнопка регистрации есть справа вверху.
Другие статьи
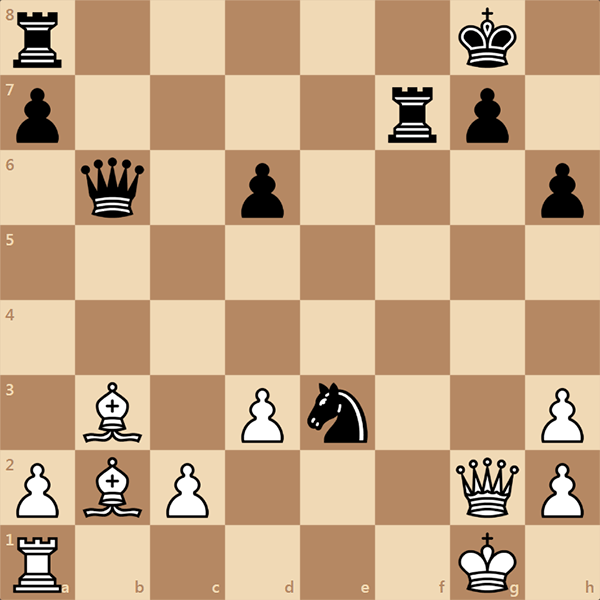
Очень интересная и полезная статья. Советуем изучить эту информация досконально. Но перед прочтением рекомендуем решить задачку. Белые начинают и ставят черным мат в 1 ход.
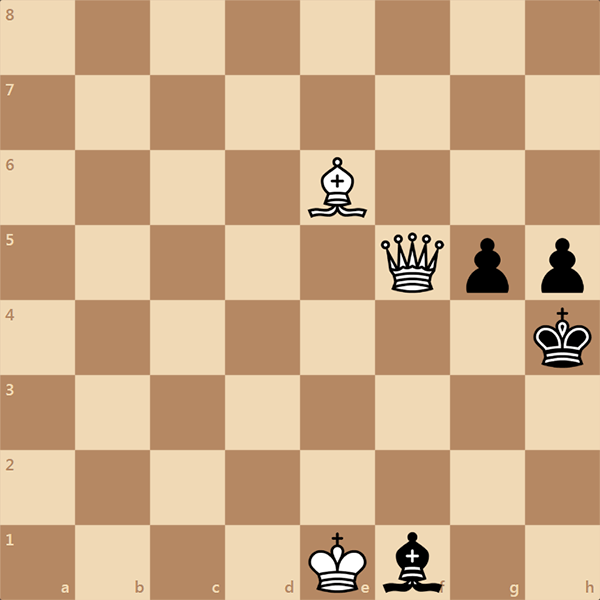
Если вы хотите научиться хорошо играть в шахматы, в первую очередь, вам нужно больше играть с более сильными соперниками, а во вторую очередь, решать больше шахматных задач. Наш сайт позволяет сделать и то, и то. Именно поэтому

В среду, 29 января 2014 года, в Цюрихе состоится сильнейший турнир в истории шахмат на сегодняшний день (средний рейтинг турнира - 2801 пункт). Пройдет турнир в отеле "Савой", а примут участие в нем 6 человек,

Турнир претендентов 2013 будет проходить в Лондоне с 14 марта по 2 апреля. Данный турнир станет самым сильнейшим в истории такого рода турниров, а его призовой фонд составит 510 000 евро! Победитель турнира

Партии онлайн в полной новости ! С 3 августа начался суперфинал чемпионата России среди женщин и мужчин, который закончится 12 августа. Все участники долго шли к этому соревнованию, и теперь сражаются друг с другом

С 19 по 26 апреля 2012 года в Киеве пройдет уже 10-й по счету мемориал Набокова - отличный международный тунир, в котором будет две группы по 10 человек - мастерский турнир и гроссмейстерский. Контроль времени 90



