Турниры
10-ка лучших шахматистов мира
Магнус КарлсенНорвегия
2864
Дин ЛижэньКитай
2806
Алиреза ФируджаФранция
2793
Каруана ФабианоСША
2783
Левон АронянРоссия
2775
Уэсли СоСША
2773
Ян НепомнящийРоссия
2766
Рихард РаппортВенгрия
2764
Аниш ГириНидерланды
2760
Максим Вашье-ЛагравФранция
2760
Головоломка по шахматам с 16 пешками

Конечно, с пешками задачи не такие разнообразные, как с другими фигурами, но все же мы нашли одну головоломку для вас, в которой участвует 16 пешек.
Условие такое: расположите 16 пешек на доске так, чтобы в одном ряду полей не находилось более трех пешек. Ряды могут быть горизонтальными и вертикальными, а также диагональными любой длины (от коротких (a6-c8) до длинных (a1-h8)) и ориентации.
3 060 просмотров
Комментарии 14
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации. Зарегистрируйтесь. Кнопка регистрации есть справа вверху.
Другие статьи
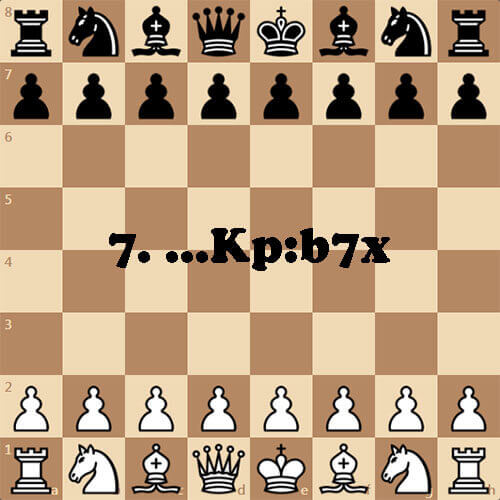
Ура, товарищ G.E. снова радует нас интересными задачами. В этот раз условие такое: партия закончилась ходом 7. ...Кр:b7x. Необходимо восстановить нотацию. Естественно, без "поддавков" тут не обойтись. Белые и черные
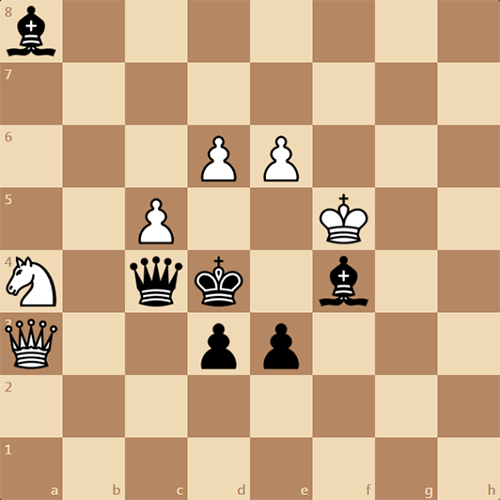
Для вас мы нашли интересную задачу, которая изображает полет Гагарина вокруг Земли. Все это происходит на шахматной доске.

У нас уже были этюды Рети, например, этот, но вот этот этюд, признаемся, мы никогда не видели. В этой позиции начинают белые и выигрывают партию. Побеждает только единственный порядок ходов. Обратите внимание на все

Первым исследователем, всерьез обратившимся к проблемам висячих пешек, был А. Нимиович, рассматривавший эту тему в своей знаменитой книге «Моя система» (ГИЗ, Москва, Ленинград, 1926). Однако первую попытку систематизировать

В средневековой азербайджанской литературе, так же как и в трактатах других восточных авторов, можно встретить интересные сообщения о правилах превращения пешек в ферзя.




