Турниры
10-ка лучших шахматистов мира
Магнус КарлсенНорвегия
2864
Дин ЛижэньКитай
2806
Алиреза ФируджаФранция
2793
Каруана ФабианоСША
2783
Левон АронянРоссия
2775
Уэсли СоСША
2773
Ян НепомнящийРоссия
2766
Рихард РаппортВенгрия
2764
Аниш ГириНидерланды
2760
Максим Вашье-ЛагравФранция
2760
Доказать легальность позиции
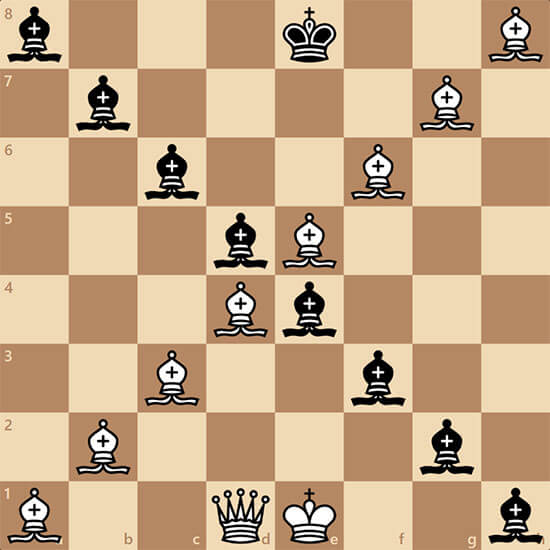
Neves прислал еще одну оригинальную задачу. вот что он пишет: "Придумал еще задачку. Она может показаться тривиальной. Но по-моему она сложная. Доказать легальность позиции"
421 просмотров
Комментарии 9
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации. Зарегистрируйтесь. Кнопка регистрации есть справа вверху.
Другие статьи
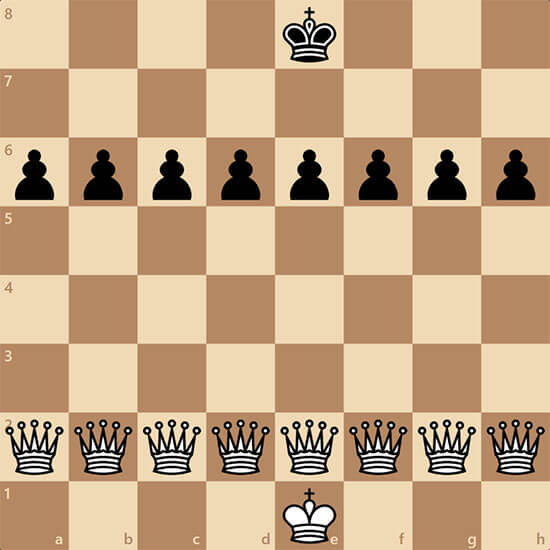
Neves прислал весьма оригинальную задачу. Вот что он пишет: "Придумал задачку. Доказать легальность позиции. Задачка простенькая. Но может быть, оригинальная?"
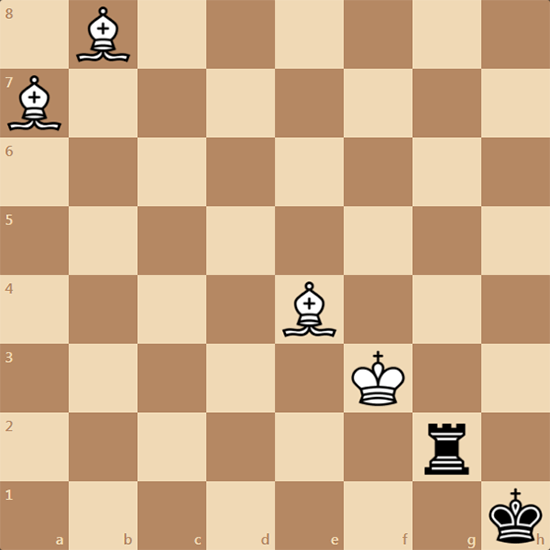
Нашли такую задачку. Пат в 3 хода. Она не сложная, зато при помощи компьютера ее не решить, как нравилось neves'у.
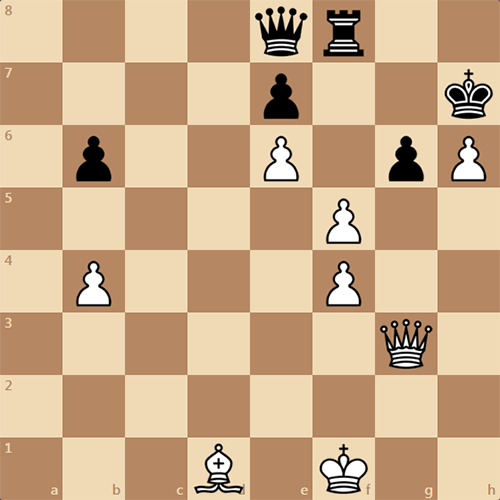
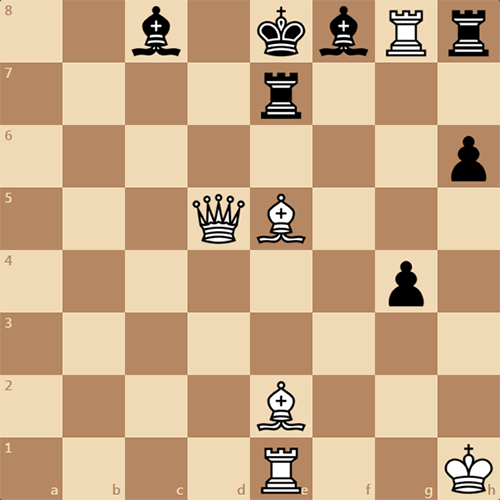
Насчет этого этюда хочется многое сказать. Так, во-первых, он, на самом деле, кажется абсолютно естественным. На доске материальное равновесие. Видно, что белые затеяли атаку на королевском фланге и пожертвовали

Приветствую всех посетителей нашего сайта! Пользователь waystrader снова прислал нам интересную задачу, которую мы сейчас и опубликуем. Задание может показаться невероятным: кооперативный ПАТ белым на
Балтийская защита - довольно сомнительный дебют на мой взгляд. Но автор данного урока хочет доказать обратное, подтвердив это конкретными вариантами. Этот дебют возникает при ходах 1.d4-d5 2.c4-Cf5 Балтийскую защиту играли Петр