Турниры
10-ка лучших шахматистов мира
Магнус КарлсенНорвегия
2864
Дин ЛижэньКитай
2806
Алиреза ФируджаФранция
2793
Каруана ФабианоСША
2783
Левон АронянРоссия
2775
Уэсли СоСША
2773
Ян НепомнящийРоссия
2766
Рихард РаппортВенгрия
2764
Аниш ГириНидерланды
2760
Максим Вашье-ЛагравФранция
2760
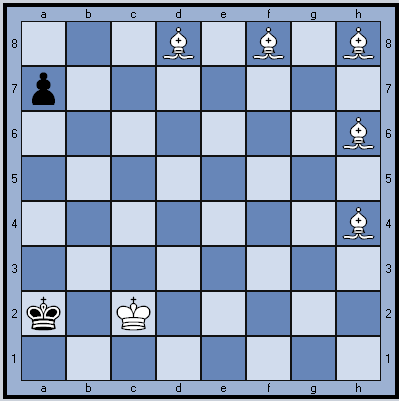
Затейливая задача со слонами

Затейливая задача со слонами - с таким заголовком пришла эта задача от Элси Ринген. Автор Harry Goldsteen, 2000. Добавить матующего слона.
635 просмотров
Комментарии 18
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации. Зарегистрируйтесь. Кнопка регистрации есть справа вверху.
Другие статьи
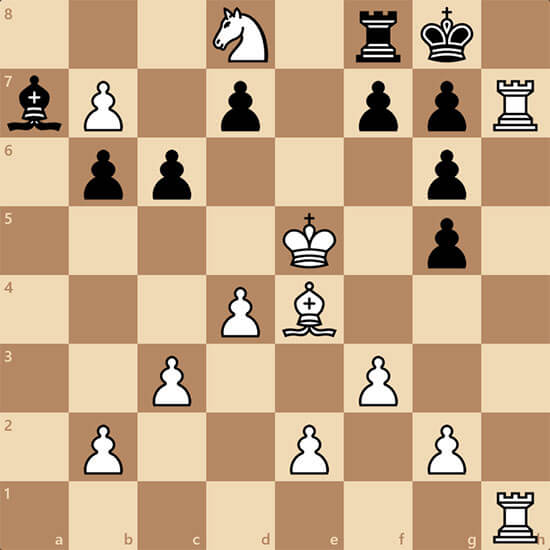
Мы вернулись. Начинаем поочередно публиковать то, что вы нам прислали. Эту задачу прислал Максим Гребенщиков персонально для Элси, но, думаем, что все примут участие в решении. Мат в 1 ход.
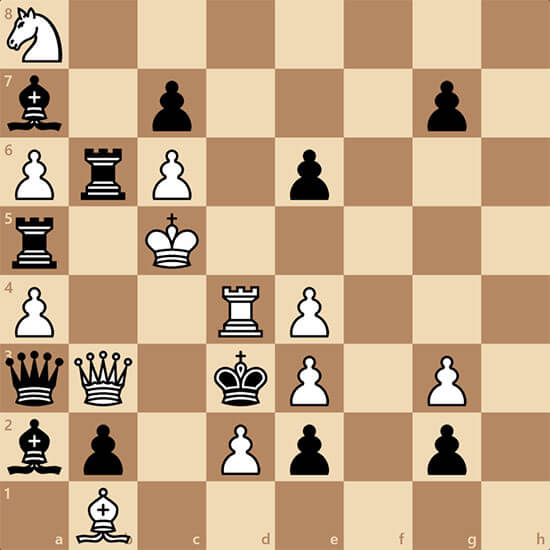
А вот и Элси Ринген подключился. Прислал такую задачу: "Задача посреди недели. Добавить фигуры и развязать позицию, автор Дмитрий Байбиков".
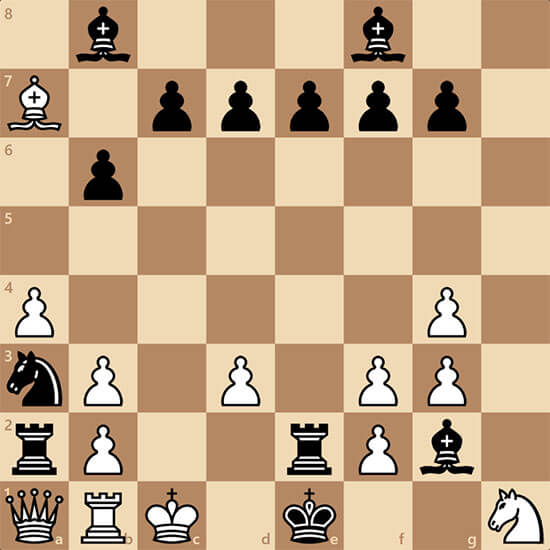
Элси Ринген прислал очень интересную задачу, автор которой Тьерри ле Глеуэр. Добавить фигуру и поставить мат в 1 ход.

Именно с таким заголовком прислал Элси Ринген задачу : "Простенькая в этот раз". Насколько она простенькая, сейчас и проверим.
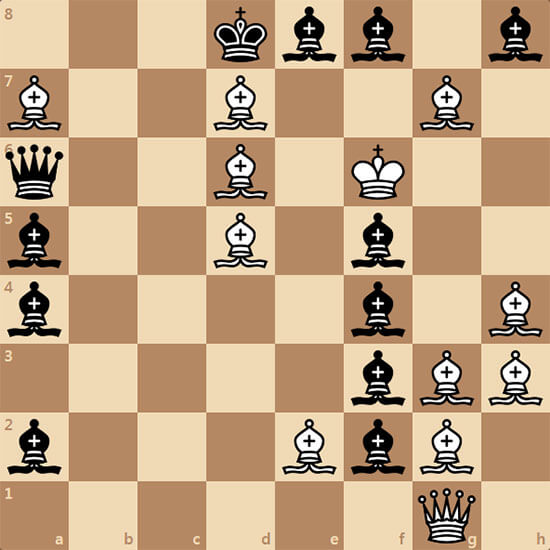
Не надо удивляться количеству слонов на доске. В прошлую среду такая позиция возникла в моей партии с контролем 3+0. Это шутка, конечно :) Автор этого творения Хью Кортни (Hugh Courtney). Белые начинают и ставят мат в 5 ходов.
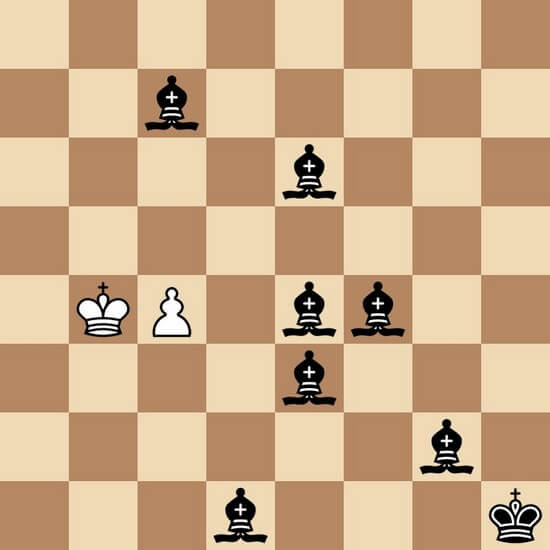
На доске 7 черных слонов это задача Даниэля Новомески (Daniel Novomesky), опубликованная в 2019 году. Серийный кооперативный мат в 12 ходов.