Турниры
10-ка лучших шахматистов мира
Магнус КарлсенНорвегия
2864
Дин ЛижэньКитай
2806
Алиреза ФируджаФранция
2793
Каруана ФабианоСША
2783
Левон АронянРоссия
2775
Уэсли СоСША
2773
Ян НепомнящийРоссия
2766
Рихард РаппортВенгрия
2764
Аниш ГириНидерланды
2760
Максим Вашье-ЛагравФранция
2760
Статья с подборкой задач от G.E.

Очень рады, что G.E. прислал новую подборку. Признаться, очень ждали и буквально вчера думали об этом. Подборка получилась великолепной и информативной.
G.E.: "После обсуждения задачи Касара, сделал вот такую полустатью-полуподборку."
Цикл Джурашевича
Самая сложная из циклических идей, связанных с переменой функций ходов белых, — это цикл Джурашевича. «Формула» этого цикла (для двухходового исполнения) выглядит следующим образом:
1.A ~ 2.B#; 1…a 2.C#
1.B ~ 2.C#; 1…a 2.A#
В рамках обычных шахмат трудность в том, что если последовательность ходов A-B ведет к некой позиции, то последовательность ходов В-А обычно приводит к ней же. Поэтому в совсем-совсем классической двухходовке (без близнецов и в стандартной паре фаз «ложный след + решение») цикл Джурашевича так и не реализован. Наилучшее к нему приближение на сегодня выглядит так:
Michel CAILLAUD, Jean-Marc LOUSTAU, Jacques ROTENBERG (Phenix 1988). Позиция после 23-го хода черных. Мат в 2 хода.

Но что не получается в двухходовке может быть сделано по-другому, например в трехходовке:
Branislav DJURASEVIC (Mat 1988). Мат в 3 хода.

Или вот так - в трехходовке варианты длиннее, так что цикл можно вложить только в решение и обойтись без ложного следа:
Zoltan LABAI, Peter GVOZDJAK (ЮТ L. Lacny-70, Pat a Mat 1996-99). Мат в 3 хода.

Кроме того, цикл можно и удлинить, например, до следующей матрицы (рекордный цикл, насколько мне известно, вообще семитактный).
1.A ~ 2.B#; 1…a 2.C; 1…b 2.D#
1.B ~ 2.C#; 1…a 2.D#; 1…b 2.A#
В вариантах трехходовки есть, например, такая реализация:
Jean-Marc LOUSTAU, Peter GVOZDJAK (Pat a Mat 2005). Мат в 3 хода.

Кроме того, при увеличении числа защит появляется возможность выстроить цикл иначе. И первый ход, и угроза все так же входят в цикл, но все немного проще. Называют такой цикла по-разному, одно из названий – «цикл Джурашевича 2» (вот так, по-простому).
Матрица цикла выглядит следующим образом (можете самостоятельно убедиться, что здесь действительно цикл):
1.A ~ 2.B#; 1…a 2.C; 1…b 2.D#
1.C ~ 2.D#; 1…a 2.B#; 1…b 2.A#
Этот цикл реализуем и в обычной двухходовке, но пока что найден только один логический механизм реализации этого цикла. Шахматных схем несколько, но они все опираются на одну и ту же логику. Вот пример:
Вячесслав КОПАЕВ (ЮТ Москва-850, Shakhmatnaya Kompozitsiya 1997). Мат в 2 хода.

Ну и, конечно, цикл интересно замкнуть, до матрицы
1.A ~ 2.B#; 1…a 2.C#
1.B ~ 2.C#; 1…a 2.A#
1.С ~ 2.A#; 1…a 2.B#
Это, наверное, самый сложный цикл для композитора и он пока что встречается только в сказочных шахматах, например (с Антицирце и сверчками):
Hubert GOCKEL (Probleemblad 2006). Мат в 2 хода. Anticirce.

Так как задача непривычная, небольшая подсказка
377 просмотров
Комментарии 4
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации. Зарегистрируйтесь. Кнопка регистрации есть справа вверху.
Другие статьи
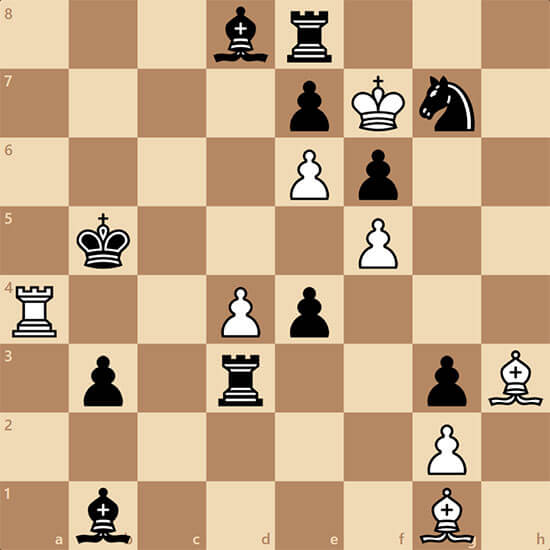
Сергей Иванович снова прислал подборку, чтобы отвлечь Ser1405 и Nevesa, и развлечь Ильфа и предлагает решить все задачи!

Чуть задержались с публикацией подборки от G.E. Постарались и сделали красиво:) Вот, что он пишет: "Мне все хочется отвлечь господина neves от сверхкомплектных позиций. Не очень они ценятся, если нет очевидных причин выхода за

Подборка задач на обратно-кооперативный мат с нейтральными фигурами. Прислал G.E., за что ему огромное спасибо. Долго оформляли, и вот, что из этого получилось.
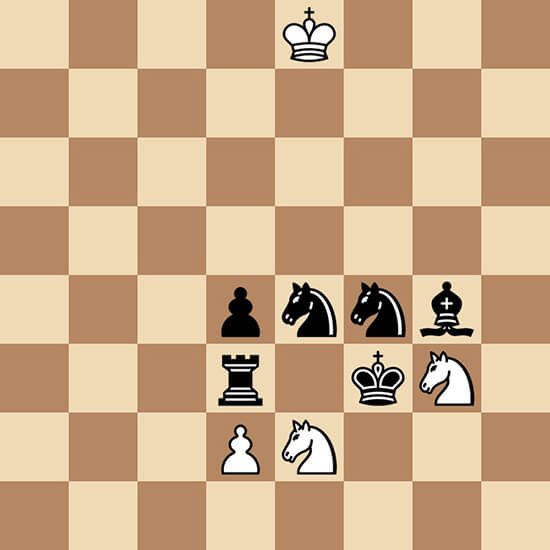
У этой задачи есть близнец, но пока давайте решим ее: кооперативный мат в 3 хода. Автор Jean-Marc Loustau, опубликована в 1993 году.
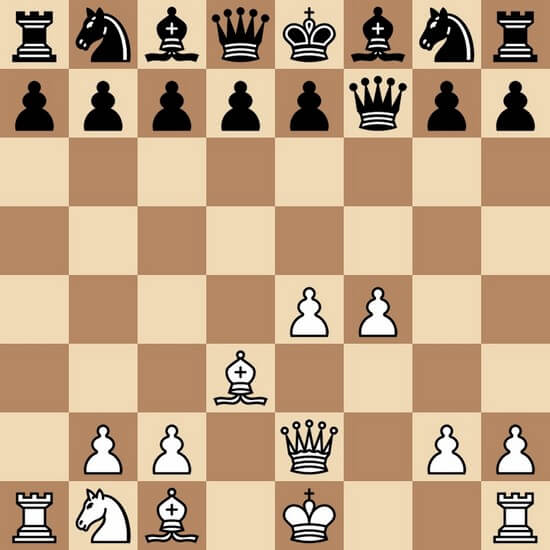
На всякий случай, расскажем правила доказательных задач (PG - Proof Game). В заданное число ходов (в нашем случае 9), нужно прийти к той позиции, что на диаграмме. И черные, и белые помогают друг другу осуществить замысел, их
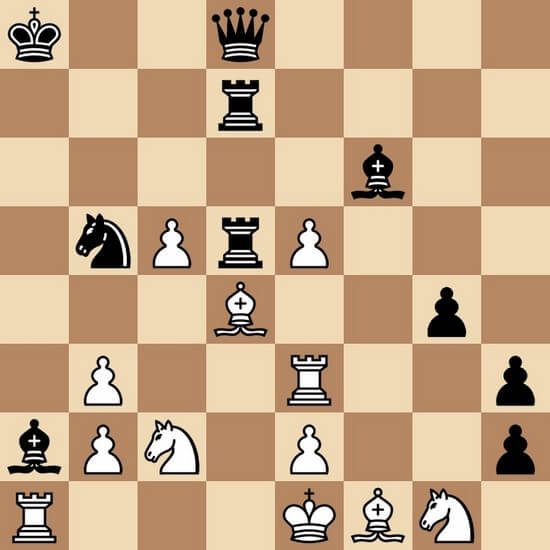
Условие этой задачи: r#2. Автор Michel Caillaud. Опубликована в 2000 году. Трудностей с решением не возникнет?




